04 HD钱包助记词生成与验证

HD钱包助记词生成与验证

1.助记词生成原理

1.1.随机熵生成 首先生成一段随机熵（Entropy）。熵的长度可以是 128 到 256 位，并且是 32 的倍数。常见的熵长度有 128 位（12 个助记词）和 256 位（24 个助记词）。每增加3个单词，

12个助记词对应128位熵，15个对应160位熵，18个对应192，21个对应224位，24个对应256，

每增加3个单词，增加32位熵，

随机熵的生成32

1.2.计算校验和 对熵进行 SHA-256 哈希计算，并取哈希值的前几位作为校验和。校验和的长度取决于熵的长度。=熵的长度 ÷ 32，除以32后得到的值就是他要校验的位数

例如，128 位熵需要 4 位校验和（因为 128 / 32 = 4），256 位熵需要 8 位校验和。160/32=5，192/32=6，224/32=7……

1.3.组合熵和校验 将校验和附加到熵的末尾，形成一个新的二进制序列。这个序列的总长度为 (熵的长度 + 校验和的长度)。

1.4.分割为助记词索引 将组合后的二进制序列分割成每组 11 位的片段，每个片段转换为一个数字，这个数字作为助记词列表中的索引。

1.5.映射为助记词 使用这些索引从预定义的 2048 个助记词列表（BIP-39 词库）中提取相应的助记词。这些助记词就是最终的助记词短语

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
# 生成助记词

# 1.1.随机熵生成
# 首先生成一段随机熵（Entropy）。熵的长度可以是 128 到 256 位，并且是 32 的倍数。常见的熵长度有 128 位（12 个助记词）和 256 位（24 个助记词）。


import hashlib
import os
import bip39

# 1.1.随机熵生成
# entropy = os.urandom(16) 
# os模块的生成16位的随机字节，这里是生成128位的熵，128位的熵就是16字节8位一个字节，128位的熵生成的是12个助记词
# 同理，如果我现在要15个词的助记词，那就是对应128+32=160位的熵，除以8位字节就是20个字节，
# 同理：如果我现在要18个词的助记词，那就是对应的160+32=192位的熵，除以8个字节就是24个字节
entropy = b'\xfb\xe50\xc5\x84\xb6\x06{.n\x12\x06SN\xb5\x82'
print(entropy)

"""
1.2.计算校验和
对熵进行 SHA-256 哈希计算，并取哈希值的前几位作为校验和。sub scrip table
校验和的长度取决于熵的长度。例如，128 位熵需要 4 位校验和（因为 128 / 32 = 4），256 位熵需要 8 位校验和
最后截取前4位出来即可
如果是128+32=160位熵，160÷32=5位校验和，那就要提取前5位出来
如果是160+32=192位熵，192÷32=6位校验和，那就要提取前6位出来
"""
#首先，hashlib.sha256(entropy)创建一个SHA-256哈希算法对象，并将entropy作为输入进行哈希计算。
# 然后，.digest()方法被调用，返回计算得到的哈希结果的二进制表示。这个二进制表示是一个字节数组（bytes），长度为32字节（256位），表示SHA-256算法对输入数据的哈希结果。
hash_bytes = hashlib.sha256(entropy).digest()
print(hash_bytes) # b's\xf7\xc9z\x88\xf0\x7f\x0f\xf0`(\xe4\xd6\x92@\xa9?\xa2os~\xbe*\x86\xe7w\x97D\xf8Z"\xb4'
# entropy_sha256[0]表示entropy_sha256的第一个字节，它是一个整数值。
# bin(entropy_sha256[0])将该整数值转换为对应的二进制字符串，返回的字符串以0b开头，例如0b11001010。
# [2:]是对二进制字符串进行切片操作，去掉开头的0b，例如11001010。
# .zfill(8)将二进制字符串填充到8位，不足的位数在开头补零，例如11001010变为11001010。
# [:4]是对二进制字符串进行切片操作，截取前4位，例如11001010变为1100。
# 结果被赋值给变量entropy_bin，表示对entropy_sha256的第一个字节进行处理后得到的二进制字符串，长度为4位。
checksum_bits = bin(hash_bytes[0])[2:].zfill(8)[:4]
print(checksum_bits) # 0111
"""
1.3.组合熵和校验
将校验和附加到熵的末尾，形成一个新的二进制序列。这个序列的总长度为 (熵的长度 + 校验和的长度)。
"""
# 这里bin(byte)后的[2:]是切掉0b开头，zfill(8)是填充，如果长度没有8位就填充0
entropy_bits = ''.join([bin(byte)[2:].zfill(8)
                       for byte in entropy])  # 这一步是生成校验和
print(entropy_bits) # 一堆0101
# 把校验和拼接到熵的末尾
combined_bits = entropy_bits + checksum_bits
print(combined_bits) # 一堆0101


"""
1.4 分割为助记词索引，等下去助记词库里面那助记词
"""
# range(0, len(combined_bits), 11)创建一个迭代范围，从0开始，每次增加11，直到达到combined_bits的长度之前的最大值。
# combined_bits[i:i + 11]是对combined_bits进行切片，从索引i开始，切片长度为11，得到一个11位的二进制字符串。
# int(combined_bits[i:i + 11], 2)将切片得到的二进制字符串作为参数传递给int()函数，并指定进制为2，将二进制字符串转换为对应的整数值。
indices = [int(combined_bits[i:i + 11], 2)
           for i in range(0, len(combined_bits), 11)] # 11是步长，[i:i+11]表示往后面取11位
print(indices)  # 这是一个列表，里面有12个数字索引，

"""
1.5 映射为助记词，就是通过上面的索引列表去助记词库里面拿到对应的助记词
"""
wordlist = bip39.INDEX_TO_WORD_TABLE  # bip39.INDEX_TO_WORD_TABLE 返回出来的是2048个助记词单词组成的元组

mnemonic = ' '.join(wordlist[index] for index in indices)
print(mnemonic)

二. 助记词验证过程

2.1 助记词验证原理 或 流程

2.1.1 检查单词数量

第一步肯定是检查单词数量，因为助记词的单词数量通常是 12、15、18、21 或 24 个单词。如果不是，则不在这些范围内。

2.2.2 检查单词是否在词表中

第二步是检查单词是否都在bip39的2048个单词的词汇表中，如果不是则错

2.2.3 将助记词转化为位串

将每个助记词的单词转换成它在bip39词汇表中对应的索引位，每个索引都表示一个11位的二进制数（0101码）

将所有的二进制数连接起来形成一个位串

2.2.4 提取种子和校验和

位串的长度应该是助记词单词数乘以11，例如12个单词的助记词对应的位串长度为132位，位串的前128位是种子，后4为是校验和。

2.2.5 计算校验和

将种子通过SHA-256哈希函数计算处一个哈希值，然后取哈希值的前4位作为计算得到的校验和。

2.2.6 验证校验和

比较提取的校验和 和 计算得到的校验和。如果两者匹配，则助记词有效，否则无效

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import bip39
def validate_mnemonic(mnemonic, wordlist):
    words = mnemonic.split()
    
    # 检查单词数量
    if len(words) not in [12, 15, 18, 21, 24]:
        return False
    
    # 检查单词是否在词汇表中
    for word in words:
        if word not in wordlist:
            return False
    
    # 将助记词转化成位串
    binary_string = ''
    for word in words:
        index = wordlist.index(word)
        binary_string += format(index, '011b') # format(index, '011b') 的含义是将 index 格式化为 11 位的二进制字符串，不足 11 位的部分在前面用零填充。
    print(binary_string)
    # 提取种子和校验和
    # 计算种子部分的长度。根据给定的单词列表 words 的长度，每个单词占用 11 位的二进制字符串，除以 3 取整数部分表示校验和的长度。通过减去校验和的长度，得到种子部分的长度。
    seed_bits_length = (len(words) * 11) - (len(words) // 3) # 
    # 从 binary_string 中提取种子部分。使用切片操作 [:seed_bits_length]，获取从开头到种子部分长度的子字符串。
    seed_bits = binary_string[:seed_bits_length]
    # 从 binary_string 中提取校验和部分。使用切片操作 [seed_bits_length:]，获取从种子部分长度开始到末尾的子字符串。
    checksum_bits = binary_string[seed_bits_length:]
    
    
    # 计算校验和
    import hashlib
    # 将种子部分的二进制字符串 seed_bits 转换为字节串。
    # 首先，使用 int(seed_bits, 2) 将二进制字符串转换为整数。
    # 然后，使用 to_bytes(len(seed_bits) // 8, byteorder='big') 将整数转换为字节串，
    # 其中 len(seed_bits) // 8 表示字节串的长度，byteorder='big' 表示使用大端字节序。
    seed_bytes = int(seed_bits, 2).to_bytes(len(seed_bits) // 8, byteorder='big')
    # 对种子字节串 seed_bytes 进行 SHA-256 哈希计算，并获取哈希结果的十六进制表示。
    # 使用 hashlib.sha256() 创建 SHA-256 哈希算法对象，然后调用 .hexdigest() 方法获取哈希结果的十六进制字符串表示。
    hash_value = hashlib.sha256(seed_bytes).hexdigest()
    # 将哈希结果的十六进制字符串 hash_value 转换为 256 位的二进制字符串。
    # 首先，使用 int(hash_value, 16) 将十六进制字符串转换为整数。
    # 然后，使用 bin() 将整数转换为二进制字符串，去掉开头的 '0b'，并使用 zfill(256) 在前面填充零，使其长度达到 256 位。
    hash_bits = bin(int(hash_value, 16))[2:].zfill(256)
    # 提取校验和部分。使用切片操作 [:len(words) // 3]，获取从二进制字符串 hash_bits 的开头到校验和长度的子字符串。校验和长度为单词列表 words 的长度除以 3。
    calculated_checksum = hash_bits[:len(words) // 3]
    
    # 验证校验和，判断助记词转换的位串与计算得来的校验和一致
    return checksum_bits == calculated_checksum

# Example usage:
mnemonic = "legal winner thank year wave sausage worth useful legal winner thank yellow"
wordlist = bip39.INDEX_TO_WORD_TABLE  # BIP-39 wordlist
is_valid = validate_mnemonic(mnemonic, wordlist)
print("Is valid mnemonic:", is_valid)

三. 编码解码过程

四. 调用 BIP-39 词库生成助记词

4.1 代码封装

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Bip39Mnemonic:
    def __init__(self):
        pass

    def createMnemonic(self, number):
        mnemonic = bip39.get_entropy_bits(number)
        return mnemonic

    def mnemonicToEntropy(self,  mnemonic):
        decode_words = bip39.decode_phrase( mnemonic)
        return decode_words
    def entropyToMnemonic(self, entropy):
        nemonic_entropy = bip39.encode_bytes(entropy)
        return nemonic_entropy

    def mnemonicToSeed(self, mnemonic):
        nemonic_to_seed = bip39.phrase_to_seed(mnemonic)
        return nemonic_to_seed

    def validateMnemonic(self, mnemonic):
        return bip39.check_phrase(mnemonic)

    def generateMnemonic(self):
        # 1. 生成 128 位随机熵 (16 字节)
        entropy = os.urandom(16)

        # 2. 计算校验和 (SHA-256)
        hash_bytes = hashlib.sha256(entropy).digest()
        checksum_bits = bin(hash_bytes[0])[2:].zfill(8)[:4]  # 取前 4 位

        # 3. 组合熵和校验和
        entropy_bits = ''.join([bin(byte)[2:].zfill(8) for byte in entropy])
        combined_bits = entropy_bits + checksum_bits

        # 4. 分割为助记词索引
        indices = [int(combined_bits[i:i + 11], 2) for i in range(0, len(combined_bits), 11)]

        # 5. 映射为助记词
        wordlist = bip39.INDEX_TO_WORD_TABLE
        mnemonic = ' '.join([wordlist[index] for index in indices])

        return mnemonic

测试：

1
2
3
4
5
6
7
8
9
10
import bip

import bip

bip39_mnemonic = bip.Bip39Mnemonic()
mnemonic_phrase = bip39_mnemonic.generateMnemonic()
print(f"Generated mnemonic phrase: {mnemonic_phrase}")

mnemonic_12_phrase = bip39_mnemonic.createMnemonic(12)
print(f"create mnemonic phrase: {mnemonic_12_phrase}")

1、助记词生成code，加密之后存储在本地设备，

2、如果要备份或导出助记词，就要把code转成助记词

3、bip39 还可以用来验证助记词是否有效。

4、助记词变成随机种子，然后再去导出

5、生成助记词的方法

bip39–

私钥对应关系

椭圆曲线是什么：

以太坊和比特币使用完全相同的椭圆曲线：secp256k1，公钥就是这个椭圆曲线上的(x, y)坐标，x，y 数值通过私钥唯一确定。

x、y 各 32 字节，故公钥为 64 字节。你可能会看到 65 字节表示的公钥，这是由 SECG 发布的行业标准的一种序列化编码方式，在最前面加一个字节的前缀，04 表示公钥为非压缩格式，即完整存储了 x 和 y 的坐标各 32 字节。

通过go语言生成私钥和公钥还有地址

1
2
3
4
5
6
7
8
9
import (
    "crypto/elliptic"
    "crypto/rand"
    "encoding/hex"

    "github.com/ethereum/go-ethereum/common"
    "github.com/ethereum/go-ethereum/crypto"
    "github.com/ethereum/go-ethereum/crypto/secp256k1"
)

生成一个椭圆曲线

1
curve := secp256k1.S256()

3 生成私钥（32byte）

1
2
3
4
5
6
7
b := make([]byte, curve.Params().N.BitLen()/8)
io.ReadFull(rand.Reader, b)
key := new(big.Int).SetBytes(b) // key就是私钥

// 打印私钥
fmt.Println("key:", len(key.Bytes()))
fmt.Println("key:", hex.EncodeToString(key.Bytes()))

4 生成公钥：对私钥进行椭圆曲线加密，生成公钥(64byte)

1
2
3
4
5
X, Y := curve.ScalarBaseMult(key.Bytes())
pubKey := elliptic.Marshal(curve, X, Y)

fmt.Println("pubKey:", pubKey)

5 生成地址：去掉公钥第一个字节04，再使用keccak256算法压缩公钥，最后的20byte就是地址

1
2
3
compressPubKey := crypto.Keccak256(pubKey[1:])
addr := common.BytesToAddress(compressPubKey[12:])
fmt.Println("addr:", addr.String())

6 验证私钥和地址匹配

将第 3 步产生的私钥导入 metamask
查看 metamask 生成的地址，和第 5 步计算出的地址是否匹配

以太坊钱包有2种

1 非确定性钱包，也叫随机钱包，每个账户通过独立的随机数生成器创建，使用keystore管理账户，没有助记词，这里不详细介绍，参考链接https://www.learnblockchain.cn/article/7070

2 分层确定性钱包，也叫HD Wallet，每个账户通过固定的种子(seed)派生，使用助记词管理所有账户。【行业标准了】

分层确定性钱包（HD Wallet）

首先看一段配置代码，看里面的几个关键信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
module.exports = {
  networks: {
    sepolia: {
      url: "...",
      accounts: {
        mnemonic: "test test test test test test test test test test test junk",
        path: "m/44'/60'/0'/0",
        initialIndex: 0,
        count: 20,
        passphrase: "",
      },
    },
  },
};

接下来3个问题：

1 mnemoic助记词如何能生成许多个账户地址？

2 path : “m/44’/60’/0’/0” 都是什么意思？为什么有些数字右上角还有小撇号？如何自定义配置他？

3 passphrase 是什么？ 有什么用？ 和metamask 的登录密码一样吗？

助记词

先导包

1
2
3
4
go get github.com/ethereum/go-ethereum/crypto // 以太坊的官方库
go get github.com/tyler-smith/go-bip32 // bip32
go get github.com/tyler-smith/go-bip39 // bip39

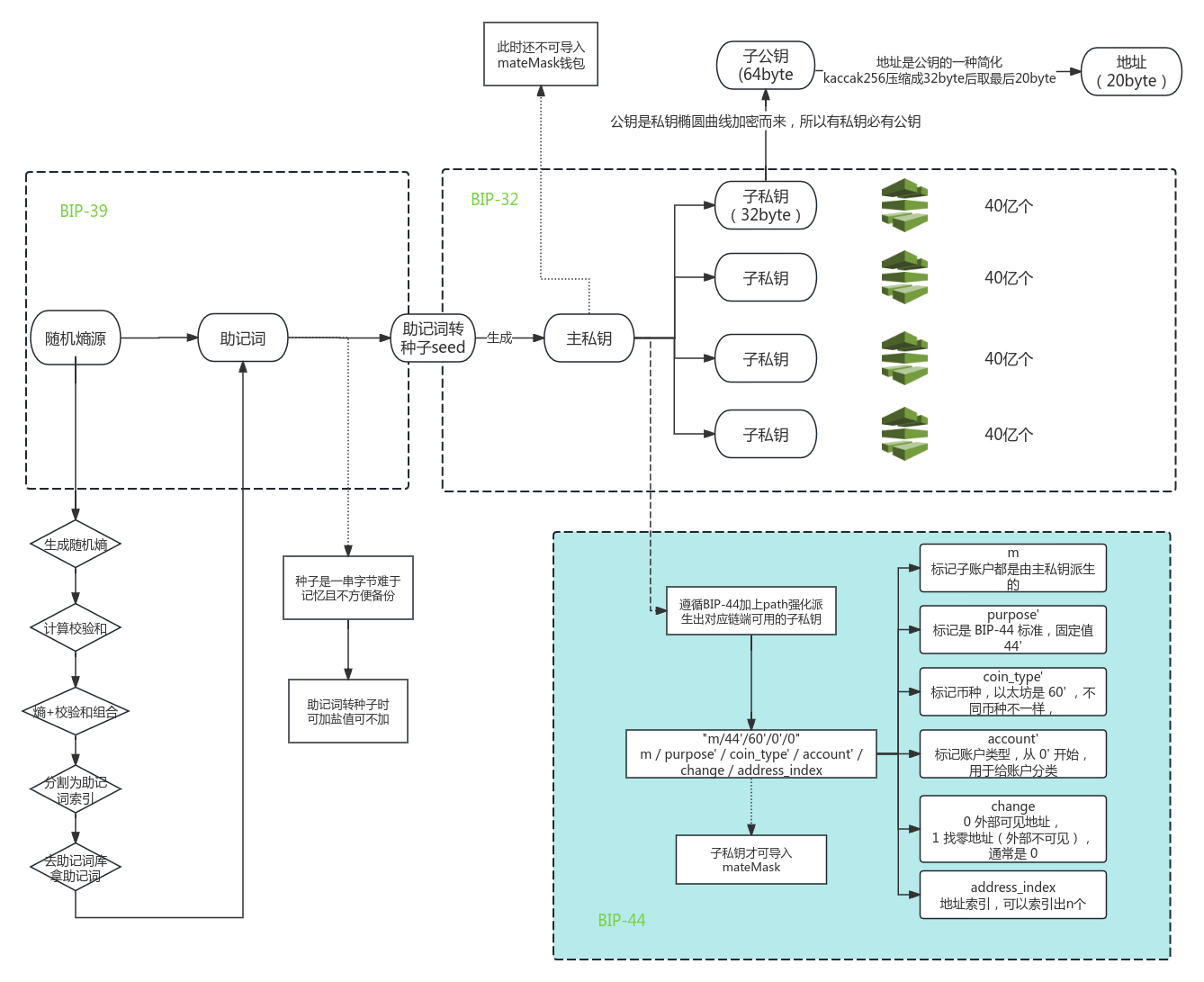
前面讲的是BIP-39提出了助记词标准，助记词是一组相对便于记忆的单词。在BIP-39的词库里面

为什么提出助记词？是为了解决BIP-32中的种子(Seed)难于记忆和不方便备份的问题，

所以BIP-39主要包含了2个功能：由熵源生成助记词，由助记词生成种子（Seed）

所以是–>BIP-39解决助记词—>BIP-32 

1
2
3
4
5
6
7
8
9
10
11
12
// 由熵源生成助记词
// @参数 128 => 12个单词
// @参数 256 => 24个单词
entropy, _ := bip39.NewEntropy(128) 
mnemonic, _ := bip39.NewMnemonic(entropy) // 这里也是参考上面的流程
// 这两行代码的原理可以参考上面的代码的流程： 熵->校验和->去头去尾拿索引->根据索引到词库拿词
fmt.Println("助记词：", mnemonic)

// 由助记词生成种子(Seed)
seed := bip39.NewSeed(mnemonic, "salt") // 问题在这里，
// 这里生成种子的方法里传了助记词和盐值进去得到种子 kaccak256压缩成32byte后取最后20byte

生成seed的时候，加入盐值的目的一是增加暴力破解的难度，二是保护种子（seed），就是即使助记词被盗了，种子也是安全的。如果设置了salt，虽然多了一层保护，但是一旦忘记了，也就代表永久丢失钱包了，所以要结合实际情况去考虑

这个盐值也叫密码口令（passphrase）,开头的hardhat配置里的passphrase就是这个盐值，和metamask的登录密码完全是两个东西。

打印下上面的代码得到的输出

1
2
3
4
助记词： alarm misery master column coach connect tower govern view then hint author
seed [173 84 238 141 106 78 98 62 46 6 144 59 166 101 230 76 224 82 219 27 19 172 10 148 144 31 24 47 33 105 201 81 182 186 46 36 235 51 91 224 123 175 170 170 111 161 117 98 60 214 91 14 204 120 213 42 250 251 126 131 85 160 213 150]
type: []uint8

可以发现：助记词是12个单词的，而Seed是一堆的字符，肯定是助记词更方便备份和恢复钱包

分层确定性钱包（HD Wallet）的基本原理

现在我们用种子生产主账户私钥，这里注意，这里的私钥还不能直接导入，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
masterKey, _ := bip32.NewMasterKey(seed)
fmt.Println("masterKey:", masterKey)
// masterKey: xprv9s21ZrQH143K4LW9szNE7QXNJkpPfFSL8k6CM9zsUb1N3czQhVFUXrZqYox2UDbgS96NrsDL2EwUzS9J6N6PfN4P3d3HNYqge6LYRQVWN6M

// 可以看下NewMasterKey的内部实现和返回内容
// NewMasterKey creates a new master extended key from a seed
func NewMasterKey(seed []byte) (*Key, error) {
	// Generate key and chaincode
	hmac := hmac.New(sha512.New, []byte("Bitcoin seed"))
	_, err := hmac.Write(seed)
	if err != nil {
		return nil, err
	}
	intermediary := hmac.Sum(nil)

	// Split it into our key and chain code
	keyBytes := intermediary[:32]
	chainCode := intermediary[32:]

	// Validate key
	err = validatePrivateKey(keyBytes)
	if err != nil {
		return nil, err
	}

	// Create the key struct，注意这个返回的key结构体，
	key := &Key{
		Version:     PrivateWalletVersion,
		ChainCode:   chainCode,
		Key:         keyBytes,
		Depth:       0x0,
		ChildNumber: []byte{0x00, 0x00, 0x00, 0x00},
		FingerPrint: []byte{0x00, 0x00, 0x00, 0x00},
		IsPrivate:   true,
	}

	return key, nil
}

首先，上面的从种子生成主账户私钥用到的就是BIP-32标准。BIP-32提出了分层确定性钱包（HD Wallet）的标准，它允许从单个种子(Seed)生成一系列相关的密钥对，报考一个主账户秘钥和无线多个子账户秘钥，不同的子账户之间具有层次关系，形成了以主账户为根节点的树形结构：

图片

由图看出，BIP-39解决熵源生成助记词—>助记词生成种子（Seed）

第二部分 BIP-32这部分的分层确定性钱包（HD Wallet），

  • 分层：分层的意思是树形结构，每一岑都有一个序号（从0开始），主账户秘钥master序号就是0，一次类推，这个叫做索引号（32位）

  • 确定性：当通过单向哈希函数派生子密钥的时候，因为即想要随机，又希望同一个父秘钥每次生成的子密钥都相同，于是，引入了链码来保证确定性，使得每次生成子密钥都是由 父秘钥 + 父链码 + 索引号 三个一起派生子密钥

  • 钱包：钱包就对应密钥（私钥+公钥）

重点：HD Wallet 的所有账户都是由 秘钥、链码、索引号（32位）三个部分组成的

所以当派生子密钥的时候，只有单独的私钥还是不行的，必须是私钥加上链码一起才能派生对应索引的子私钥，因此私钥和链码放在一起也叫做扩展私钥，为啥？因为是可拓展的，同样的，公钥和链码放一起叫做扩展公钥，接下里看下主账户拓展私钥masterKey来派生子账户（注意哦，主私钥+链码=拓展私钥）

1
2
3
4
5
6
7
8
9
10
11
12
// 由主账户私钥生成子账户私钥
// @参数 索引号
childKey1, _ := masterKey.NewChildKey(1)
fmt.Println("childKey1:", childKey1)

// 派生第二个子账户
childKey2, _ := masterKey.NewChildKey(2)
fmt.Println("childKey2:", childKey2)
// 输出结果,可以看到开头是xprv开头的，
//childKey1: xprv9vmc7bbX7qbvBfGPKLctPka9JcchdCkwh9NrxPdVjZfGjLyM3RHGsTWwyrXGr86ADJDanyrMKLhJNbuua5fC5tv7XPVF4zBDoQiNYN69rFP
// childKey2: xprv9vmc7bbX7qbvEwJfuMa9S1K9F1iuMTeaAaYcbg7NLVGViM6VTbyPecWXiMG37QgKrS4Myz9d9N5QjTmbTgAjFZzsdwGaWuhnBMewz2mFCKd

这里看一下NewChildKey方法内部逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// NewChildKey derives a child key from a given parent as outlined by bip32
func (key *Key) NewChildKey(childIdx uint32) (*Key, error) {
	// Fail early if trying to create hardned child from public key
	if !key.IsPrivate && childIdx >= FirstHardenedChild {
		return nil, ErrHardnedChildPublicKey
	}

	intermediary, err := key.getIntermediary(childIdx) // 这个方法内部通过 `父密钥`+`父链码`+`索引号`派生了子密钥
	if err != nil {
		return nil, err
	}

	// Create child Key with data common to all both scenarios
	childKey := &Key{
		ChildNumber: uint32Bytes(childIdx),
		ChainCode:   intermediary[32:], // 索引号，intermediary数组右边的32位
		Depth:       key.Depth + 1, // 这里就是链码
		IsPrivate:   key.IsPrivate,
	}
    ........
    childKey.Key = addPrivateKeys(intermediary[:32], key.Key) // 子密钥，intermediary数组的左边32位


	return childKey, nil //  返回出去

代码总结：派生出的字节数组 左边32字节是秘钥，右边32字节就是链码

除了通过拓展私钥派生出子私钥，还可以通过拓展公钥派生出子公钥。不过需要注意的是：公钥只能派生出子公钥，无法派生出子私钥。下面验证一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 用主账户公钥 派生 子账户公钥（没有私钥）
publicKey := masterKey.PublicKey() // 这里是拿到主账户公钥，待会下面会派生
fmt.Println("publicKey:", publicKey)

PubKeyToChild, _ := publicKey.NewChildKey(1) // 通过主账户公钥派生出子账户公钥
fmt.Println("PubKeyToChild:", PubKeyToChild)
// 输出
// publicKey: xpub661MyMwAqRbcEkC8JkXwGBm4jX1FmphgcYjyhnKXbW4QKA1DAX5V1Hp6SoCKev4Gim8AqSYzM7ZCttjsHb7SNSH4ufkgsWGVupS73DLxr7Z
// PubKeyToChild: xpub68shoUguHPvUVptKbW1BrWa1eAvX5rVKUEQ8S9e3fPVvr5EVhXkVBbNvKJBFR1TqFrmqRERkELB6tixWjc8VouZz3HZRCq2YZBnoLsEfkdx

// 用主账户私钥，派生出子账户私钥，再生产子账户公钥，然后判断一下是否一致
childKey1, _ := masterKey.NewChildKey(1) // 派生子账户1
publicKey1 := childKey1.PublicKey() // 从子账户1的秘钥恢复出公钥来，
fmt.Println("publicKey3:", publicKey1) // 打印下这个子账户1公钥
fmt.Println(bytes.Equal(PubKeyToChild.Key, publicKey1.Key)) // 返回的ture，和签名我们生成的是一样的
// publicKey3: xpub68shoUguHPvUVptKbW1BrWa1eAvX5rVKUEQ8S9e3fPVvr5EVhXkVBbNvKJBFR1TqFrmqRERkELB6tixWjc8VouZz3HZRCq2YZBnoLsEfkdx

首先再重复一下，要明确的是，公钥只能派生子公钥，无法派生出子私钥，但是私钥确可以推出公钥

就会有2种派生方式：

  • 1、拓展公钥（公钥+链码）父公钥==> 子公钥，子私钥另外由父私钥派生，不归公钥管
  • 2、拓展私钥（私钥+链码）父私钥===>子私钥 ===> 子公钥

第一种方式好处就是：可以用父公钥暴露在外面，然后可以派生出n多个子公钥用于接收资产，因为没有私钥，所以只能接收，不能花费（签名）所以很安全，与此同时，在另一个地方用子私钥来控制资产（签名），这样就做到了子公钥和子私钥的解耦，

但是这样的派生方式有很大的危险，就是如果有人拿到了这个子私钥，那么则可以通过子私钥+父链码来推导出父私钥，父私钥拿到了就可以加上其他的链码来推导其他姊妹账户，于是就出现了强化派生（Hardened derivation）强化派生限制了父公钥派生出子公钥的能力，只能使用第二种派生也就是 父私钥===>子私钥===>子公钥

HD Wallet 有规定：

索引号在0到2^32-1(0x0 to 0x7FFFFFFF)之间只用于常规派生

索引号在2^31到2^32-1(0x80000000 to 0xFFFFFFFF)之间只用于强化派生

PS：在表示中，强化派生密钥右上角有一个小撇号，如：索引号为 0x80000000 就表示为 0’

接下来回头去看下上面的派生子密钥的源码，也就是上面的NewchildKey方法，里面有一个判断，就是判断你的入参childIdx 是在哪个索引范围，如果是在强化派生的索引范围，就是强化派生，就不允许公钥派生

1
2
3
4
5
6
7
8
func (key *Key) NewChildKey(childIdx uint32) (*Key, error) {
    // Fail early if trying to create hardned child from public key
    // 这里就可以看到，如果这个childIdx >= FirstHardenedChild 就会返回空且抛出错误
    if !key.IsPrivate && childIdx >= FirstHardenedChild {
       return nil, ErrHardnedChildPublicKey
    }
    .....
}

接下来就是由公钥去生成地址了，这里就是签名提到的压缩的过程，这个简单不需要额外理解，

1
2
3
4
5
6
// 由公钥推出地址（解压缩的过程，就是转化然后去头去尾的）
// 先解压缩公钥，再去推地址
pubKey1, _ := crypto.DecompressPubkey(PubKeyToChild.Key)
// 生成子账户地址
addre1 := crypto.PubkeyToAddress(*pubKey1)
fmt.Println("addre1:", addre1)

但是！但是！但是！ 你现在走到这一步，还是不可以导入到metaMask钱包里面的。需要继续往下走

分层确定性钱包（HD Wallet）的标准路径

还记得本文开头提出的那个问题吗？

path的"m/44'/60'/0'/0" 都是什么意思？现在你知道了，右上角的小撇号代表强化派生，现在来看其他部分。

BIP-44 确定了 HD 钱包的标准路径。由于 HD 钱包的树状结构，每一层有 40 亿个子密钥（20 亿个常规子密钥和 20 亿个强化子密钥），层数可以无限扩展，没有尽头。

导致钱包里账户的路径可能性是无穷的，假设你想从 metamask 更换到另一个不同的钱包应用，就会存在兼容性问题。

于是乎，BIP-44 定义了标准，只要遵循了这个标准的钱包之间都是兼容的。好消息是，包括 metamask 在内的许多钱包，都遵循了这个标准，第三个BIP来了，签名助记词是BIP39，种子是BIP32

BIP-44 标准的钱包路径（path）参数：m / purpose’ / coin_type’ /account’ change / address_index

  • m ：标记子账户都是主私钥派生而来的。
  • purpose’ ：标记是 BIP-44, 固定值是 44’
  • coin_type’ ：标记账户类型，从 0’ 开始，用于给账户分类===> 完整的币种类型
  • change ：0 外部可见地址，1 找零地址（外部不可见），通常默认0
  • address_index ：地址索引

注意：为了保护主私钥安全，所有主私钥派生的第一级账户，都采用强化派生。

但是，你可以使用m/0，m/1'/0，m/0'/1/2/3这种任何路径你都可以随便输入，派生出来的都是正确的账户，只是这些不符合标准的钱包不一定能兼容的了这些链，且安全性不可知，所以统一准信行业标准（BIP-44）

实现一个以太坊的钱包（一个符合BIP-44标准的路径path）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 所以这个masterKey 的来源还要再写一遍
助记词==>种子==> 主私钥masterKey
// 这里的masterKey是什么？是主私钥，然后主私钥经过各种派生之后，生成的子私钥
// 以太坊的币种类型是60
// FirstHardenedChild = uint32(0x80000000) 是一个常量
// 以路径（path: "m/44'/60'/0'/0/0"）为例
key, _ := masterKey.NewChildKey(bip32.FirstHardenedChild + 44)  // 这一步是在做强化派生， 对应 purpose' 44是符合BIP-44标准
key, _ = key.NewChildKey(bip32.FirstHardenedChild + uint32(60)) // 还是强化派生，对应 coin_type类型60'
key, _ = key.NewChildKey(bip32.FirstHardenedChild + uint32(0))  // 还是强化派生，对应account
key, _ = key.NewChildKey(uint32(0))                             // 常规派生，对应 change
key, _ = key.NewChildKey(uint32(0))                             // 常规派生，对应的 address_index

// path已经完毕，生成地址
ethPublicKey, _ := crypto.DecompressPubkey(key.PublicKey().Key)
fmt.Println("ethPublicKey:", ethPublicKey)
ethAddre := crypto.PubkeyToAddress(*ethPublicKey).Hex()
fmt.Println("ethAddre:", ethAddre)
// 尝试打印一下这个key的私钥算
fmt.Println("key:", key.Key)                 // 这个时候你直接打印Key是十进制的字节切片
privateKeyHex := hex.EncodeToString(key.Key) // 这里在做的就是转化成16进制的字符，
fmt.Println("key:", privateKeyHex)

所以这里总结一下，助记词–私钥–公钥–地址，这个过程中做了什么？

privatekeyprocess

blockChain
#block #实战
04 HD钱包助记词生成与验证
http://example.com/2024/05/25/04HD钱包助记词生成/
作者
Wangxiaowang
发布于
2024年5月25日
许可协议