【python】读书笔记之性能测算和大O算法分析（十三）

第 13 章　性能测量和大O算法分析

　　对于大多数小型程序而言，性能可能没那么重要。我们也许会花一小时来为任务编写一个自动化脚本，而这个脚本只要几秒钟就能运行完。就算时间再长一些，也不过是我们端着咖啡杯回到办公桌旁的时长。

　　有些情况下，对于花时间学习如何提升脚本速度要持谨慎态度，因为我们需要先学习程序的运行速度测量方法，否则无法知道所做的修改是否提升了程序的速度。而这就是Python模块timeit和cProfile的用武之地。这些模块不仅可以测量代码的运行速度，还会生成一个配置文件，说明代码的哪些部分已经足够快，哪些部分仍需改进。

　　除了测量程序的速度，你还将在本章学习如何测量理论上因程序需要处理的数据增加，程序运行时间随之增加的增速。在计算机科学领域中，它被称为大O记法。缺乏传统计算机科学背景的软件开发人员可能有时会觉得自己的知识储备不够全面。尽管计算机科学教育颇有成果，但对软件开发的直接作用可能有限。我曾开玩笑（但也不无道理）地说，大O记法占了我学位中80%的有用内容。本章对这个实用话题进行了介绍。

13.1　timeit模块

　　“过早优化是万恶之源”是软件开发领域中的一句俗语。（这句话经常被认为是出自计算机科学家高德纳，但他又将其归功于计算机科学家Tony Hoare。Tony Hoare则认为这归功于高德纳。）过早优化，也就是在知道具体需要优化的内容前盲目地进行优化，往往表现在程序员试图通过巧妙的方式来节省内存或编写更快的代码。一个例子是使用XOR算法来交换两个整数值，而不是使用额外的临时变量：

>>> a, b = 42, 101 # 设置两个变量
>>> print(a, b)
42 101
>>> # 通过一系列 ^ XOR运算交换它们的值：
>>> a = a ^ b
>>> b = a ^ b
>>> a = a ^ b
>>> print(a, b) # 目前两个值已经被交换了
101 42

　　如果你不熟悉XOR算法（该算法使用^位运算符），那么这段代码看起来会很神秘。使用巧妙的编程技巧的弊端在于它会产生复杂、不可读的代码。我们应该记住“Python之禅”的原则之一——“可读性很重要”。

　　更糟糕的是，这可能只是你自以为的巧妙之举。你不能总是一拍脑门儿就认为一个精巧的编程方法更快，而将被它取代的旧代码很慢。只有测量并比较运行时间（运行一个程序或一段代码所需的时间）才是证明快速与否的唯一方法。要知道运行时间的增加意味着程序在变慢，也就是程序需要更多的时间来做同样的工作。有一个类似的概念，我们有时也将程序的运行时间简称为运行时（runtime）。“这个错误发生在运行时”意味着错误发生在程序运行期间，而非程序被编译成字节码时。

　　Python标准库的timeit模块会将待测量的一小段代码运行数千次，甚至数百万次，以确定平均运行时间。timeit模块还可以暂时禁用自动垃圾回收器，以避免其对运行时间造成的差异。如果想测试多行代码，可以传递一个多行代码字符串，或者使用分号分隔多行代码：

>>> import timeit
>>> timeit.timeit('a, b = 42, 101; a = a ^ b; b = a ^ b; a = a ^ b')
0.1307766629999998
>>> timeit.timeit("""a, b = 42, 101
... a = a ^ b
... b = a ^ b
... a = a ^ b""")
0.13515726800000039

　　在我的计算机上，XOR算法运行这段代码只需要大约0.1秒，这个速度够快吗？来和使用额外临时变量的整数交换代码对比一下：

>>> import timeit
>>> timeit.timeit('a, b = 42, 101; temp = a; a = b; b = temp')
0.027540389999998638

　　出乎意料吧？使用额外变量不仅可读性更好，而且速度也快了两倍。巧妙的XOR技巧可能会节省几字节的内存，但代价是减慢了速度并降低了代码可读性。牺牲代码的可读性来减少几字节的内存使用或者纳秒级别的运行时间并不值当。

　　更好的做法是使用多重赋值技巧交换两个变量，也叫作迭代解包。它的速度更快：

>>> timeit.timeit('a, b = 42, 101; a, b = b, a')
0.024489236000007963

它在可读性和速度两方面都是最好的。这个结论不是拍脑门儿想出来的，而是出于客观的测量。

　　timeit.timeit()函数也可以接受第二个字符串类型参数，用作初始化代码。初始化代码仅在最初运行一次。也可以传递一个整数作为数字关键字参数改变默认的试验次数。比如，下面的测试测量了Python的random模块生成10 000 000个1到100的随机数需要多长时间（在我的计算机上需要大约10秒）：

>>> timeit.timeit('random.randint(1, 100)', 'import random', number=10000000)
10.020913950999784

　　默认情况下，传递给timeit.timeit()的代码字符串不能访问程序其他部分的变量和函数：

>>> import timeit
>>> spam = 'hello' # 定义spam变量
>>> timeit.timeit('print(spam)', number=1) # 测量打印spam的时间
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "C:\Users\Al\AppData\Local\Programs\Python\Python37\lib\timeit.py",
line 232, in timeit
    return Timer(stmt, setup, timer, globals).timeit(number)
  File "C:\Users\Al\AppData\Local\Programs\Python\Python37\lib\timeit.py",
line 176, in timeit
    timing = self.inner(it, self.timer)
  File "<timeit-src>", line 6, in inner
NameError: name 'spam' is not defined

为了解决这个问题，可以将globals()1的返回值作为globals关键字参数：

1Python内置函数的作用是以字典类型返回全部全局变量。——译者注

>>> timeit.timeit('print(spam)', number=1, globals=globals())
hello
0.000994909999462834

　　编写代码的一个有效准则是先让它跑起来，再让它快起来。只有当你有了一个能用的程序后，你才需要专注于它的效率，让它变得更高效。

13.2　cProfile分析器

　　timeit模块对测量小的代码片段很有效，但cProfile模块在分析整个函数或程序时更具优势。

　　程序分析可以系统性地分析程序的运行速度、内存使用情况等。cProfile模块是Python的分析器，用于测量程序的运行时间和程序内各个函数调用消耗的时间。这些信息为代码提供了更细粒度的测量结果。

　　要使用cProfile分析器，请将待测量的代码串传递给cProfile.run()。来看看cProfile是如何测量和报告一个短函数的执行情况的。该函数的作用是将1到1 000 000的数字进行求和运算：

import time, cProfile
def addUpNumbers():
    total = 0
    for i in range(1, 1000001):
        total += i

cProfile.run('addUpNumbers()')

运行该程序得到的输出是这样的：

      4 function calls in 0.064 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
     1    0.000    0.000    0.064    0.064 <string>:1(<module>)
     1    0.064    0.064    0.064    0.064 test1.py:2(addUpNumbers)
     1    0.000    0.000    0.064    0.064 {built-in method builtins.exec}
     1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

　　每一行标注了不同的函数花费的时间。cProfile.run()的输出中的列的解释如下。

• **ncalls**：对函数的调用次数。
• **tottime**：该函数花费的总时间，注意不包括在子函数中花费的时间。
• **percall**：tottime除以调用次数。
• **cumtime**：在该函数及其子函数内花费的累计时间。
• **percall**2：cumtime除以调用次数。
• **filename:lineno(function)**：该函数所在的文件及行号。

2注意这个名字跟前面一样，并非存在错误。——译者注

　　比如，你可以从No Starch的网站上下载rsaCipher.py和al_sweigart_pubkey.txt。这个RSA密码程序在《Python密码学编程》中有所提及。在交互式shell中输入以下内容，以分析encryptAndWriteToFile()函数对由'abc'*100000表达式创建的30万个字符长的信息的加密过程：

>>> import cProfile, rsaCipher
>>> cProfile.run("rsaCipher.encryptAndWriteToFile('encrypted_file.txt', 'al_sweigart_pubkey. txt', 'abc'*100000)")
         11749 function calls in 28.900 seconds

   Ordered by: standard name

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.001    0.001   28.900   28.900 <string>:1(<module>)
        2    0.000    0.000    0.000    0.000 _bootlocale.py:11(getpreferredencoding)
--snip--
        1    0.017    0.017   28.900   28.900 rsaCipher.py:104(encryptAndWriteToFile)
        1    0.248    0.248    0.249    0.249 rsaCipher.py:36(getBlocksFromText)
        1    0.006    0.006   28.873   28.873 rsaCipher.py:70(encryptMessage)
        1    0.000    0.000    0.000    0.000 rsaCipher.py:94(readKeyFile)
--snip--
     2347    0.000    0.000    0.000    0.000 {built-in method builtins.len}
     2344    0.000    0.000    0.000    0.000 {built-in method builtins.min}
     2344   28.617    0.012   28.617    0.012 {built-in method builtins.pow}
        2    0.001    0.000    0.001    0.000 {built-in method io.open}
     4688    0.001    0.000    0.001    0.000 {method 'append' of 'list' objects}
--snip--

可以看到，传递给函数cProfile.run()的代码共运行了28.9秒。注意这个示例中运行总时间最多的函数。Python内置函数pow()花了28.617秒，几乎等于总耗时！我们没法改变pow()的代码（因为它是Python的内置函数），但也许可以改变程序的代码以减少对它的调用。

　　在这个示例中，这是不可能的，因为rsaCipher.py已经经过充分的优化。不过对这段代码的分析还是让我们了解到pow()是主要瓶颈。因此，试图改进readKeyFile()等函数（该函数的运行时间很短，cProfile将其时间报告为0）是没有意义的。

　　阿姆达尔定律（Amdahl’s Law）体现了这一思想，其计算了其中一个组件得到改进的情况下对整个程序的运行速度的增益。该公式为整个任务的速度=1/((1-p)+(p/s))，其中s是一个组件的速度提升，p是该组件在整个程序中的比例。比如将一个在程序中占总运行时间90%的组件速度提升一倍，结果是1/((1-0.9)+(0.9/2)) = 1.818，也就是说整个程序的速度提升了约82%。这比将一个只占总运行时间25%的组件的速度提升3倍要好，它的结果是1/((1-0.25)+(0.25/2))=1.143，也就是整体速度提升了约14%。你不需要背整个公式，只要记住将代码中运行时间长的代码速度提升一倍，要比将已经够快的代码速度提升一倍更有效。这是一个常识：昂贵的房子打9折要比便宜的鞋子打9折更有诱惑力。

13.3　大O算法分析

　　大O是一种算法分析形式，它描述了代码如何应对处理规模的增长。它将代码分为几个等级，笼统地描述代码的运行时间随着处理工作量的增加而需要增加的时间。Python开发者Ned Batchelder将大O描述为对“代码如何随着数据增长而变慢”的分析。这也是他在PyCon 2018上的演讲主题。

　　假设这样一个情景：你有一些工作需要一小时才能完成，如果工作量增加一倍，需要花多少时间才能完成工作？你可能会说两小时，但实际上答案取决于工作的类型。

　　如果读一本薄书需要一小时，那么读两本薄书大概就要两小时。如果你能在一小时内将500本书按照书名的字母顺序排列，将1000本书按照字母顺序排列花费的时间就不止两小时，因为你必须在更大的图书集合中为每本书找到正确的位置。如果工作只是检查书架是否是空的，那么书架上无论有0本、10本还是1000本都无所谓。只要看一眼就会立刻知道答案。无论有多少本书，需要的时间都是差不多的。尽管不同的人在阅读或者编排字母时的速度存在个体差异，但总体来说趋势是一样的。

　　算法的大O描述了这种趋势。大O描述算法的总体表现与执行该算法的实际硬件速度的快慢无关。大O不使用任何具体的单位（比如秒或者CPU周期)来描述算法的运行时间，因为运行时间在不同的计算机或编程语言之间会有差异。

13.4　大O阶

　　大O记法通常有以下几个等级，它们的顺序是从低到高，也就是从随着数据量增长速度减慢最少的代码到速度减慢最多的代码：

　　(1) O(1)，恒定时间（最低)

　　(2) O(\log n)，对数时间

　　(3) O(n)，线性时间

　　(4) O(n\log n)，N-Log-N时间

　　(5) O(n^2)，多项式时间

　　(6) O(2^n)，指数时间

　　(7) O(n!)，阶乘时间（最高）

　　注意，大O阶使用了以下符号：一个大写的O，后面是一对小括号，括号中是对阶数的描述。大写的O表示阶数（order）。n表示代码要处理的输入数据的大小。

　　使用大O记法无须理解对数、多项式等词的精确的数学意义。下一节将详细描述这些阶数，这里先给出简化的解释：

• O(1)算法和O(\log n)算法很快；
• O(n)算法和O(n\log n)]算法还不错；
• O(n^2)算法、O(2^n)算法和O(n!)算法很慢。

　　当然你可以找出反例，但大多数情况下，上述结论是对的。还有很多大O阶未被列出，这里给出的是最常用的。现在逐个看看每个阶数所描述的任务种类。

13.4.1　使用书架打比方描述大O阶

　　在下面的大O阶例子中，我将继续使用书架的比喻。n指的是书架上的书的数量，大O阶描述了随着书的数量的增加，各种任务所花费的时间是如何增加的。

1. O(1)，恒定时间

   找到“书架是否是空的”的答案是恒定时间的操作。书架上到底有多少书并不重要，只要看一眼就能判断书架是否是空的。做出这个判断所用的时间与书的数量多少无关，因为只要看到书架上有一本书，就可以停止寻找了。因为n值与执行任务的时间无关，所以O(1)中并不包含n。有时，恒定时间也被写作O(c)。

2. O(\log n)，对数时间

   对数是指数的逆运算：指数[2^4，也就是2 × 2 × 2 × 2，等于16。而对数 log_2(16（读作以2为底16的对数）等于4。在编程中，我们一般使用2作为对数基数，所以将O(\log_2n简写为O(\log n)。

   在一个按照字母顺序排列的书架上搜索某本书是一个对数时间的操作。为了找到一本书，你可以先检查在书架中间位置的那本书。如果它就是你要找的书，那么任务就完成了。如果不是，你要确定想找的书是在中间这本书的前面还是后面。这么做可以有效地将找书范围缩减至一半。接下来不断重复这个过程，在一半范围内检查处于中间位置的书。这被称为二分搜索算法，13.5.2节中有一个示例。

   ​

   将一组书分为两半的次数一共是log_2n次。在一个有16本书的书架上，最多需要4步就能找到想找的书，因为每一步都会将需要继续搜索的书的范围缩减一半。如果书架上的书增加一倍，也只需要多搜索一次。如果一个书架按照字母顺序排列有42亿本书，也只需要32步就能找到某本书。

   O(\log n)算法通常包括一个划分和消化的步骤，即从n个输入中选择一半进行处理，再从这一半中选择一半，以此类推。log n运算的可扩展性很好：工作量增加一倍，运算时间只增加一步。

3. O(n)，线性时间

   阅读书架上的所有书是一个线性时间的操作。如果书的厚度差不多，将书架上的书的数量增加一倍，那么读完所有书就需要大约两倍的时间。运算时间与书的数量n成比例增加。

4. O(n\log n)，N-Log-N时间

   将一组书按照字母顺序排序是一个N-Log-N时间的操作。这个阶数是O(n)和O(\log n)的运行时间相乘的结果。可以将O(n\log n)]的任务看成一个需要被执行n次的O(\log n)任务。下面对原因做一个通俗的解释。

   我们有一摞需要按照字母顺序排列的书和一个空书架。按照前文描述的二分搜索算法的步骤，找到书架上某本书的位置是O(\log n)的操作。如果有n本书需要按字母顺序排列，而每本书按照字母顺序排列都需要log n步，按照字母顺序排列整个书架需要的步骤就是n x log n，或者 log n x n。如果书的数量变成原来的两倍，将所有书按照字母顺序排列也只需要两倍多一点的时间。所以O(n\log n)]算法的增长速度是较慢的。

   事实上，所有高效的排序算法都是O(n\log n)]的：合并排序、快速排序、堆排序和TimSort。（TimSort是由Tim Peters发明的，Python的sort()方法使用的就是该算法。）

5. O(n^2)，多项式时间

   在一个没有排序的书架上检查是否存在重复的书是一个多项式时间的操作。如果有100本书，那么你可以从第一本开始，拿起来跟其他99本书比较，看看是否相同。接着拿起第二本、第三本……分别和其他99本书比较，检查一本书是否跟其他书重复需要99个步骤（四舍五入成100，也就是这个示例中的n）。而我们需要对每本书都进行一次操作，也就是一共100次。因此检查书架上是否存在重复书的步骤大约是n x n ，也就是n^2。（即使我们足够聪明，不去重复比较，也需要执行近n^2步。)

   运行时间以增加的图书数量的平方成比例增加。检查100本书中是否有重复需要10 000步（100 × 100）。而检查两倍于这个数量的书，也就是200本书，则需要40 000步（200 × 200），即以前的4倍。

   根据我自己的实际编码经验，大O分析最常见的用途是避免在问题存在O(n\log n)]或O(n)的算法时意外地编写一个O(n^2)算法。O(n^2)阶意味着算法的速度随着规模增加急剧下降。如果你的代码是O(n^2)阶或更高，应该先暂停，思考是否可能有另一种算法能够更快地解决问题。为了应对这种问题，无论是在大学里还是在网上，学习数据结构和算法课程会有所帮助。

   O(n^2)也被称为二次方时间。算法的复杂度还可能是O(n^3)，即立方时间，或者O(n^4)，即四次方时间，又或者是其他多项式时间。它们的速度随着指数的增大而变慢。

6. O(2^n)，指数时间

   给书架上所有书的组合拍照是一个指数时间的操作。想象一下：书架上的每本书要么在照片中，要么不在照片中。图13-1显示了n为1、2、3时的所有组合。如果n为1，会有两张照片：有书或没书。如果n为2，则有4张照片：两本书都在书架上、两本书都不在、第一本书在而第二本不在、第二本书在而第一本不在。当数量增加到3本书时，你要做的工作又增加了一倍：你需要对两本书的每个子集中再考虑第三本书在（4张照片）或不在（另外4张照片）的情况（一共是8张照片，因为2^3=8。每增加一本书，工作量就增加一倍。如果有n本书，需要拍摄的照片数量（也就是工作量）是2^n。

   

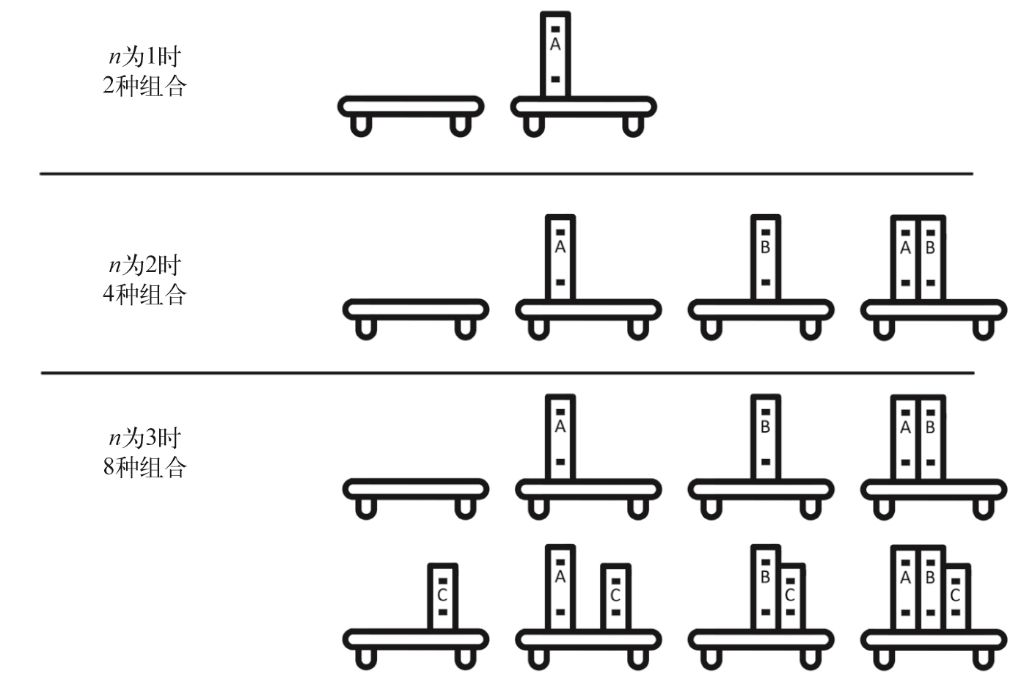
   图13-1　书架上有一本、两本、三本书时的所有组合

   指数级任务的运行时间增加得很快。6本书需要2^6即64张照片，32本书则需要2^32即超过42亿张照片。O(2^n)、O(3^n)、O(4^n)等虽然阶数不同，但时间复杂度都属于指数级。

   ​

7. O(n!)，阶乘时间

   把书架上的书按照所有顺序拍照是一个阶乘时间的操作。这些书的所有顺序被称为n本书的排列组合，结果是n!，也就是n的阶乘。一个数字的阶乘是不超过该数的所有正整数的乘积。比如3是3 × 2 × 1，即6。图13-2展示了3本书可能出现的所有排列组合。

   

   图13-2　书架上3本书的全部6种排列组合

   思考如何得到n本书的每种排列组合。第一本书有n种可能的选择；第二本书有n-1种可能的选择（除了第一本书之外的每一本书都可以被选作第二本）；第三本书有n-2种选择，以此类推。当有6本书时，就存在6!种选择，也就是6 × 5 × 4 × 3 × 2 × 1，即720张照片。而再增加一本书，结果就是7!，即5040张照片。即使n值并不大，阶乘时间的算法也很快变得不能在合理时间内完成。如果你有20本书供排列，就算1张照片的拍摄时间只有1秒，它仍然需要比宇宙存在的时间还要长的时间拍摄完所有排列组合。

   一个著名的O(n!)问题是旅行商问题。一个销售员要访问n个城市，希望计算出他需要访问的n个城市不同顺序的旅行总距离，再根据其计算结果确定旅行总距离最短的访问顺序。在城市很多时，该任务被证明无法很快完成，但幸运的是，优化算法可以找到一条相对距离较短（但不保证是最短）的路线，运算所用时间要比O(n!)短得多。

13.4.2　大O测量的是最坏情况

　　大O专用于测量任务的最坏情况。比如要在一个无序的书架上找到一本特定的书，你需要从一头开始搜寻，直到找到它。你可能很幸运，查看的第一本书就是你要找的书。但你也可能不走运，查看的最后一本书才是你要找的书，或者它根本就不在书架上。因此，在最好的情况下，即使书架上有几十亿本待搜索的书也无所谓，反正你会立刻找到要找的书。但是这种乐观的态度对算法分析来说毫无意义。大O描述的是在不幸运的情况下发生的事情：如果书架上有n本书，那么你将不得不查看完所有书。在这种情况下，运行时间的增加速度与书的数量增加的速度相同。

　　一些程序员还会使用大Omega符号描述算法的最佳情况。比如，一个!\mathit{\Omega}(n)算法在最好的情况下会具有线性效率。而在最坏的情况下，它可能表现得更慢。有些算法会遇到特别幸运的情况，即不需要做任何工作。比如，任务是找到前往目的地的驾驶路线，而你就在目的地。

　　大Theta符号则表示算法的最好情况和最坏情况下的阶数相同。比如，\mathit{\Theta}(n)描述了一个在最好情况和最坏情况下都具有线性效率的算法，也就是说，它既是O(n)算法，也是\mathit{\Omega}(n)算法。在软件工程中，这些符号不如大O常用，但你还是应该知道它们。

　　在谈论“平均情况下的大O”时，人们指的是大Theta；在谈论“最佳情况下的大O”时，指的是大Omega，这并不稀奇。他们的说法严格来说是矛盾的。大O具体指的是一个算法的最坏情况下的运行时间。但即使他们的措辞在技术上不正确，你也应该能够理解他们的意思。

理解大O所需的数学知识

　　如果你对代数生疏了，复习以下数学知识就足以帮助你进行大O分析。

• 乘法：加法的重复，2 × 4 = 8就相当于2 + 2 + 2 + 2 = 8。使用变量进行抽象，!n+n+n相当于3 x n。
• 乘法符号：在代数中，乘法符号×经常被省略。2 x n会被写作!2n。当操作数都是数字时，2 × 3会被写作2(3)，即6。
• 乘法同一性：一个数乘以1结果是这个数本身。如5 × 1 = 5，42 × 1 = 42。更笼统的描述是：n x 1=n。
• 乘法分配律：2 × (3 + 4) = (2 × 3) + (2 × 4)，等式两边都等于14。更笼统的描述是：a(b + c) = ab + ac。
• 幂是重复的乘法：[2^4=16（读作2的4次方等于16）。这和2 × 2 × 2 × 2 = 16一样。这个示例中的2是基数，4是指数。使用变量进行抽象，n x n x n x n相当于n^4]。在Python中，我们使用**运算符表示幂运算：2**4的结果是16。
• 1次方的结果就是基数本身，如2^1=2，9999^1=9999。更笼统的描述是：n^1=n。
• 0次方的结果都是1，如2^0=1，9999^0=1。更笼统的描述是：n^0=1。
• 系数是乘法因数：在3n^2+4n+5中，系数是3、4、5。可以看到，5被视为系数的原因是它可以被写作5(1)，即5n^0。
• 对数是幂运算的逆运算：由于2^4=16，因此\log_2(16)=4，它的念法是“以2为底16的对数是4”。在Python中，我们使用math.log()函数求解：math.log(16, 2)的结果为4.0。

　　计算大O时经常需要通过合并同类项来简化方程。项是一些数字和变量相乘的组合：在3n^2+4n+5中，项是3n^2、4n和5。同类项是指它们的变量及指数都相同。在表达式3n^2+4n+6n+5中，项4n和6n是同类项。可以将该表达式简写成3n^2+10n+5。

　　请记住，由于n x 1=n，像3n^2+5n+4这样的表达式可以被认为是3n^2+5n+4(1)。这个表达式中的项与大O阶的O(n^2)、O(n)和O(1)类似。这一点在后面为大O的计算舍弃系数时会出现。

　　当你首次学习计算一段代码的大O时，这些数学规则可能会派上用场。但在完成13.5.4节的学习后，你可能就不需要它们了。大O是一个简单的概念，即使没有严格遵循数学规则，依然能衡量算法的快慢。

13.5　确定代码的大O阶

　　确定一段代码的大O阶需要进行4项工作：确定n是什么，计算代码中的步骤数，去除低阶项，去除系数。

　　比如，为下面的readingList()函数计算大O阶：

def readingList(books):
    print('Here are the books I will read:')
    numberOfBooks = 0
    for book in books:
        print(book)
        numberOfBooks += 1
    print(numberOfBooks, 'books total.')

　　回顾一下，n代表代码处理的输入数据的规模。在函数中，n几乎总是作为参数。readingList()函数的唯一参数是books，所以books的大小似乎是n的一个很好的候选项，因为books越大，函数运行的时间就越长。

　　接下来计算这段代码中的步骤数。步骤的定义是模糊的，将一行代码视为一个步骤是个不错的规则。循环有多少步，最终的步骤数量就等于迭代次数乘以循环体中的代码行数。为了方便理解，下面给出readingList()函数内的代码的步骤数：

def readingList(books):
    print('Here are the books I will read:')     # 1步
    numberOfBooks = 0                            # 1步
    for book in books:                           # 单次循环内的步骤数 * n
        print(book)                              # 1步
        numberOfBooks += 1                       # 1步
    print(numberOfBooks, 'books total.')         # 1步

除了for循环，每行代码都被视作一个步骤。for循环对于books中的每一项都会执行一次，因为books的规模是n，所以它执行了n步。不仅如此，for循环内的所有步骤也被一并执行了n次。因为循环中共有两个步骤，所以总步骤数是2 x n。可以这样描述步骤：

def readingList(books):
    print('Here are the books I will read:')     # 1步
    numberOfBooks = 0                            # 1步
    for book in books:                           # n * 2 步
        print(book)                              #（已归并计算）
        numberOfBooks += 1                       #（已归并计算）
    print(numberOfBooks, 'books total.')         # 1步

　　计算总步骤数时，得到的结果就是1+1+(n\times2)+1。这个表达式可以简写为2n+3。

　　大O并不会用来描述具体细节，它只是一个笼统的指标。所以我们可以去掉低阶项。2n+3中的阶数包括线性阶(2n)和常数阶(3)，我们保留最大的阶数，也就是2n。

　　接下来，我们从中去除系数。2n的系数是2，去掉它后就只剩下n。最终readingList()函数的大O阶是O(n)，也就是线性时间复杂度。

　　这个阶数应该是经得起推敲的。函数运行中有很多步骤，总体来说，如果books列表的数量增大10倍，运行时间也会增大到10倍左右。将图书从10本增加到100本，增加前的步骤数为1 + 1 + (2 × 10) + 1，即23步，而增加后则为1 + 1 + (2 × 100) + 1，即203步。203大约是23的10倍，所以运行时间确实是随着n的增加成比例地增加了。

13.5.1　为什么低阶项和系数不重要

　　我们在步骤的计算过程中删除了低阶项，因为随着n的增长，它们变得不那么重要。如果将前面提到的readingList()函数中的books规模从10增加到10 000 000 000（100亿），那么步骤数将从23增加到20 000 000 003。由此可见，当n足够大时，额外多的3步影响不大。

　　当数据量增加时，低阶项即使有较大的系数也不足以造成太大影响。当n的值一定时，高阶复杂度的代码总是比低阶的运算慢。假设有一个名为quadraticExample()的函数，其算法复杂度为O(n^2)，具体步骤数为3n^2。同时，另有一个名为linearExample()的函数，其算法复杂度为O(n)，具体步骤数为1000n。系数1000比系数3大，但起不了什么作用，随着n的增加，最终O(n^2)平方运算会变得比O(n)线性运算慢。实际代码是什么样并不重要，可以假设代码如下所示：

def quadraticExample(someData):  # someData的规模是n
    for i in someData:           # n步
        for j in someData:       # n步
            print('Something')   # 1步
            print('Something')   # 1步
            print('Something')   # 1步

def linearExample(someData):     # someData的规模是n
    for i in someData:           # n 步
        for k in range(1000):    # 1 * 1000 步
            print('Something')   # （已归并计算）

与quadraticExample()的系数（3）相比，linearExample()的系数很大（1000）。如果输入n的大小为10，那么O(n^2)函数只需要300步，而O(n)函数则需要10 000步，前者快很多。

　　需要注意的是，大O记法主要关注的是算法在工作量较大时的性能。当n达到334或以上的规模时，quadraticExample()函数总是比linearExample()函数慢。即使linearExample()有1000000n步，一旦n达到333 334，quadraticExample()函数仍然会是更慢的那个。而在某些时候，O(n^2)的运算会比O(n)或阶数更低的运算慢。为了说明这种情况，请看图13-3中的大O阶的图示。这张图展示了所有主要的大O阶。x轴代表n，即数据的规模，y轴代表进行运算所需要的运行时间。

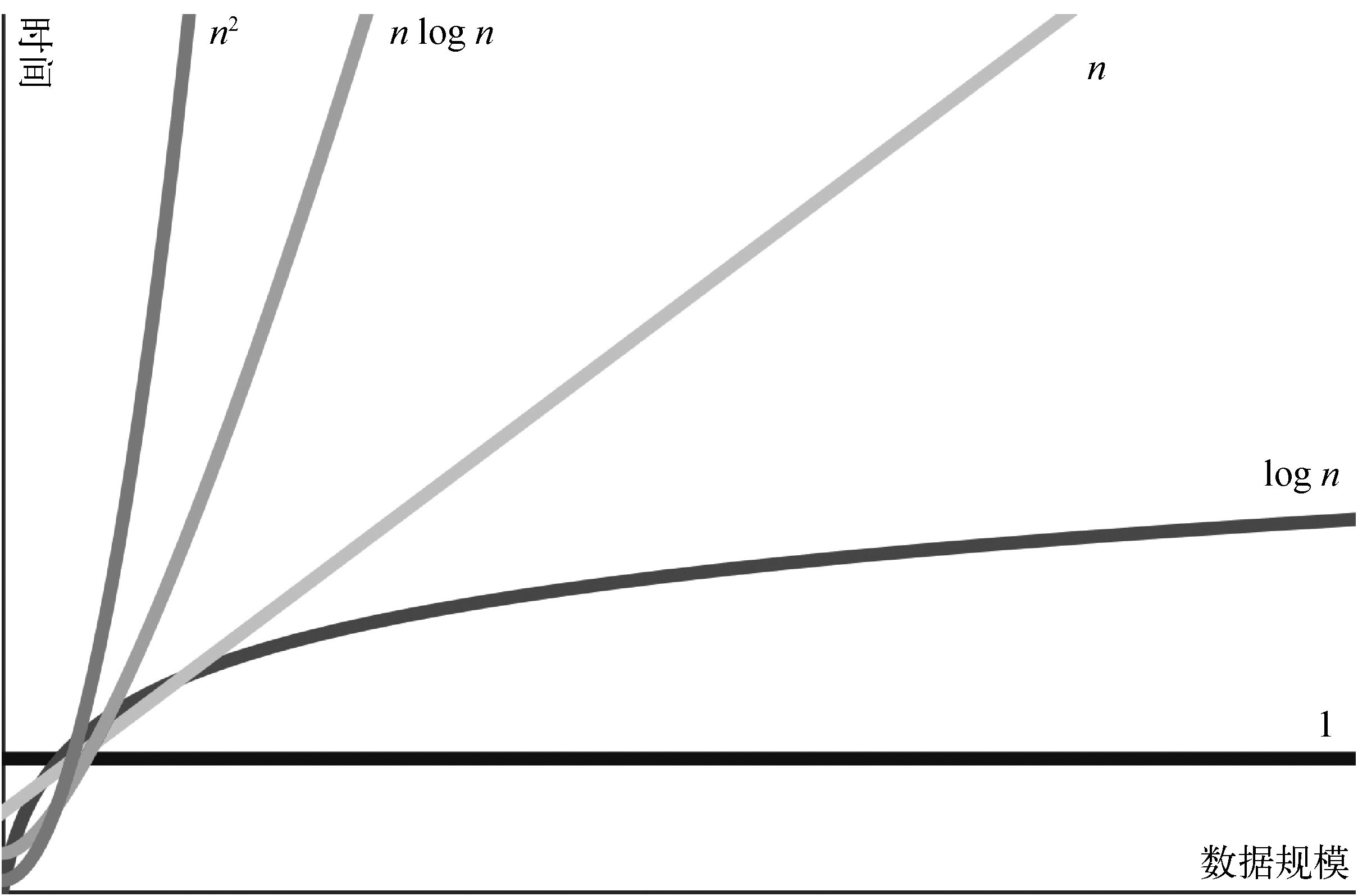
图13-3　大O阶图示

　　如图13-3所示，高阶复杂度的运行时间比低阶的运行时间增长得快。虽然低阶因有大系数会暂时大于高阶，但高阶的运行时间最终还是会超过它们。

13.5.2　大O分析实例

　　让我们确定示例函数的大O阶。示例会使用一个名为books的参数，它是一个包含书名字符串的列表。

　　countBookPoints()函数根据books中的书计算出一个分数。大多数的书为1分，某位作者的书为2分：

def countBookPoints(books):
    points = 0                        # 1步
    for book in books:                # 单次循环内的步骤数 * n
        points += 1                   # 1步

    for book in books:                # 单次循环内的步骤数 * n
        if 'by Al Sweigart' in book:  # 1步
            points += 1               # 1步
    return points                     # 1步

　　步骤数为1+(n x 1)+(n x 2)+1，合并同类项后变成3n+2，去掉低阶项和系数后则为O(n)，也就是线性复杂度。无论在books中循环1次、2次还是10亿次，复杂度都是O(n)。

　　到目前为止，所有的单层循环示例都具有线性复杂度，那是因为这些循环迭代了n次。但接下来的示例会说明，代码中仅有一层循环并不意味着一定具有线性复杂度，尽管对数据进行迭代的循环本身是线性的。

　　iLoveBooks()函数打印了“I LOVE BOOKS!!!”和“BOOKS ARE GREAT!!!”各10次：

def iLoveBooks(books):
    for i in range(10):              # 单次循环内的步骤数 * 10
        print('I LOVE BOOKS!!!')     # 1步
        print('BOOKS ARE GREAT!!!')  # 1步

该函数有一个for循环，但并非是对books列表的循环，无论books的大小如何，它都要执行20步。我们可以将步骤数改写为20(1)，去掉系数20后就变成了O(1)，即恒定的时间复杂度。这是对的，无论books列表的大小如何，该函数都需要相同的运行时间。

　　接下来，假设有一个cheerForFavoriteBook()函数，它的作用是在books中搜索一本最喜欢的书：

def cheerForFavoriteBook(books, favorite):
    for book in books:                            # 单次循环内的步骤数 * n
        print(book)                               # 1步
        if book == favorite:                      # 1步
            for i in range(100):                  # 单次循环内的步骤数 * 100
                print('THIS IS A GREAT BOOK!!!')  # 1步

for book循环在books列表上进行迭代，进行的步骤数为n乘以每次循环内的步骤数。该循环又包含了一个嵌套的for i循环，它迭代了100次。这意味着for book循环运行了102 x n次，也就是102n次。去掉系数后可以发现，cheerForFavoriteBook()仍然只是一个O(n)的线性操作。系数102看起来很大，怎么能忽略呢？但是请仔细想想：如果favorite压根儿不在books中，这个函数就只会运行1n步。系数的影响很不固定，所以它们对于算法复杂度的计算来说没有意义。

　　下一个示例，findDuplicateBooks()函数为每本书（线性操作）在books列表中搜索一次（也是线性操作）：

def findDuplicateBooks(books):
    for i in range(books):                     # n步
        for j in range(i + 1, books):          # n步
            if books[i] == books[j]:           # 1步
                print('Duplicate:', books[i])  # 1步

for i循环遍历整个books列表，在每个循环内执行n步操作。for j循环对books列表的部分进行迭代，当去除系数时，也可以将其视为线性操作。也就是说，for i循环进行了n x n步操作，也就是n^2。这使得findDuplicateBooks()成为O(n^2)的多项式操作。

　　遇到嵌套循环并不都意味着它就是多项式操作，只有当两个循环都迭代n次时才是。这导致了n^2步，代表这是O(n^2)的操作。

　　来看一个具有挑战性的示例。前文提到过二分搜索算法，它的工作原理是在一个有序列表（我们称之为haystack）的中间位置检查是否存在某个特定的项目（我们称之为needle）。如果不存在，则继续搜索haystack的前一半或者后一半，这取决于待搜索项目的位置相较于中间位置的项目是更靠前还是更靠后。我们会不停重复这个过程，搜索一半的一半的一半……直到找到needle或者断定它不在haystack中。注意，二分搜索只有在列表中的项目是有序的时候才有效。

def binarySearch(needle, haystack):
    if not len(haystack):                                        # 1步
        return None                                              # 1步
    startIndex = 0                                               # 1步
    endIndex = len(haystack) - 1                                 # 1步

    haystack.sort()                                              # ???步

    while start <= end:                                          # ???步
        midIndex = (startIndex + endIndex) // 2                  # 1步
        if haystack[midIndex] == needle:                         # 1步
            # 找到needle
            return midIndex                                      # 1步
        elif needle < haystack[midIndex]:                        # 1步
            # 搜索前一半
            endIndex = midIndex - 1                              # 1步
        elif needle > haystack[mid]:                             # 1步
            # 搜索后一半
            startIndex = midIndex + 1                            # 1步

　　binarySearch()中有两行不易计算步数的代码。haystack.sort()调用的大O阶取决于Python的sort()方法内的代码。这段代码不容易找到，不过还是可以经网上查找得知它是O(n\log n)]操作。所有一般的排序函数至少是O(n\log n)]操作。13.5.3节将介绍几个常见的Python函数和方法的大O阶。

　　while循环不像之前我们看到的for循环那样容易分析。我们必须先了解二分搜索算法，确定该循环共有多少次迭代。在循环开始前，startIndex和endIndex分别在haystack的头和尾，midIndex被设置在haystack范围的中点。在while循环的每次迭代中，有两件可能发生的事情。如果haystack[midIndex] == needle，我们就找到了needle，函数会返回needle的索引。如果needle < haystack[midIndex]或needle > haystack[midIndex]，则将startIndex和endIndex所覆盖的范围减半。范围减半可以通过调整startIndex或endIndex来实现。我们将长度为n的列表分为一半的次数有\log_2(n)次（这是一个数学常识）。因此，while循环的阶数较大，是O(\log n)。

　　由于haystack.sort()行的O(n\log n)]阶大于O(\log n)阶，因此我们舍去较小的O(\log n)，整个binarySearch()函数为O(n\log n)]阶。如果可以保证binarySearch()只会在haystack为有序列表时调用，那就可以删除haystack.sort()行，使binarySearch()成为一个O(\log n)阶函数。从技术上看，这确实提高了函数的效率，但整个程序的效率并未提升，因为这种做法只是将必要的排序工作转移到了程序的其他部分。大多数二分搜索的实现省略了排序的步骤，因此二分搜索算法被视为具有O(\log n)的复杂度。

13.5.3　常见函数调用的大O阶

　　对代码进行大O分析必须考虑它调用的任何函数的大O阶。如果它们是你写的，你当然可以直接分析自己的代码。但对于Python内置函数和方法的大O阶，你必须参考下面的列表。

　　这个列表包含了Python序列类型，比如字符串、元组和列表的一些常见操作的大O阶。

• s[i]读和s[i] = value赋值是O(1)操作。
• **s.append(value)**是O(1)操作。
• **s.insert(i, value)**是O(n)操作。在一个序列中插入值（特别是在前面）需要将索引大于i的所有项在序列中向后移动一个位置。
• **s.remove(value)**是O(n)操作。从一个序列中移除值（特别是在前面）需要将索引大于i的所有项在序列中向前移动一个位置。
• **s.reverse()**是O(n)操作，因为序列中的每一项都必须被重新排列。
• **s.sort()**是O(n\log n)]操作，因为Python的排序算法具有O(n\log n)]阶。
• **value in s**是O(n)操作，因为必须检查每一项。
• **for value in s**是O(n)操作。
• **len(s)**是O(1)操作，因为Python会额外记录一个序列中有多少项，所以当它被传递给len()时，不需要进行重新计算。

　　下面这个列表包含了Python映射类型，比如字典、集合和不可变集合的一些常见操作的大O阶。

• m[key]读和m[key] = value赋值是O(1)操作。
• **m.add(value)**是O(1)操作。
• **value in m**对字典而言是O(1)操作，比在序列中使用快得多。
• **for key in m**是O(n)操作。
• **len(m)**是O(1)操作，因为Python会自动跟踪映射中的项数，所以当它被传递给len()时，不需要进行重复计算。

　　列表需要从头到尾逐个搜索项，而字典使用键计算值的地址，查找某个键对应的值的时间是不变的。这种计算的过程被称为哈希算法，计算所得的地址则被称为哈希值。哈希算法超出了本书的范围，它是许多映射操作能保持O(1)恒定时间的原因所在。集合也会使用哈希算法，因为它本质上是只有键而非键−值对的字典。记住，将列表转换为集合是一个O(n)操作，所以先将列表转换为集合，再访问集合中的项对于提升效率而言毫无意义。

13.5.4　一眼看出大O阶

　　一旦熟悉了大O分析，通常就不用按照步骤一步步做了。一段时间后，你就可以在代码中寻找一些蛛丝马迹以快速确定大O阶。

　　记住，n是代码处理的数据量。这里有一些通用规则。

• ​
• 如果代码不访问数据，阶数就是O(1)。
• ​
• 如果代码遍历数据，阶数就是O(n)。
• ​
• 如果代码有两个嵌套的循环，每个循环都对数据进行迭代，阶数就是O(n^2)。
• ​
• 函数调用不能只算作一个步骤，而是要计算该函数内部代码的步骤。可以查阅13.5.3节。
• ​
• 如果代码中存在重复将数据规模减半再处理的步骤，阶数就是O(\log n)。
• ​
• 如果代码中对于数据中的每一项都有进行分治再处理的步骤，阶数就是O(n\log n)]。
• ​
• 如果代码遍历数据中所有可能的值的组合，阶数就是O(2^n)或其他指数级。
• ​
• 如果代码查看了数据中每个可能的值的排列组合，阶数就是O(n!)。
• ​
• 如果代码涉及对数据排序，那么阶数至少是O(n\log n)]。

　　这些规则可以当作很好的分析起点，但它们不能代替实际的大O分析。需要记住，大O阶不是对代码的速度快慢、是否高效的最终判断。思考下面这个waitAnHour()函数：

import time
def waitAnHour():
    time.sleep(3600)

　　从技术上讲，waitAnHour()函数的时间复杂度是固定的O(1)。一般会认为固定时间复杂度的代码是快速的，但它的运行时间是一小时！这是否意味着这段代码效率低？不，实际上你不可能编写出一个运行时间比一小时还短的waitAnHour()函数。

　　大O并不是代码分析的全部，它的意义在于使你了解代码在遇到越来越多的输入数据时会有怎样的表现。

13.5.5　当n很小时，大O并不重要，而n通常都很小

　　掌握了大O记法的知识后，你可能迫不及待地想对你写的每一段代码进行分析。在你开始使用这个工具来敲掉眼中钉前，请记住，仅当有大量数据需要处理时，大O分析才有价值。而在现实问题中，数据量通常很小。

　　在这种情况下，费尽心思设计大O阶较低的复杂算法可能并不值得。Go语言编程设计者Rob Pike提出过5条关于编程的规则，其中一条就是“当n小的时候，花哨的算法会很慢，而n通常是小的”。大多数程序员不会面对大规模的数据中心或者复杂的计算，而是处理更普通的程序。在这种情况下，在分析器下运行代码会比进行大O分析产出更多有关代码性能的具体信息。

13.6　小结

　　Python标准库中有两个用于分析代码的模块：timeit和cProfile。timeit.timeit()函数在运行并对比小段代码的速度差异时比较有优势。而cProfile.run()函数可以为较大的函数编写出详细的报告，指出其瓶颈所在。

　　测量代码性能很重要，不要臆断。虽然可以使用巧妙的技巧来提升程序的效率，但这种做法可能会让程序更慢。为了避免花费不必要的时间优化程序中不重要的部分，阿姆达尔定律在数学上给出了解决方案，该公式描述了一个组件的效率提升对整个程序的增益。

　　大O是程序员在计算机科学中使用最广泛的实用概念。这需要一些数学知识才能理解，但明白一些基本概念就可以衡量代码是如何随着数据增长而变慢的，这并不需要进行大量的数字运算。

　　常见的大O阶有7种：O(1)，即恒定时间，指随着数据n的大小增长而不发生变化的代码；O(\log n)，即对数时间，指随着n翻倍而增加一步的代码；O(n)，即线性时间，描述的是随着n的增长成比例变慢的代码；O(n\log n)]，即线性对数时间，描述的是比O(n)慢一点的代码，许多排序算法是这个阶数；O(n^2)，即多项式时间（平方），指代码的运行时间以n输入数据的平方增加；O(2^n)，即指数时间；O(n!)，即阶乘时间。阶乘时间并不常见，但会出现在涉及组合或排列组合的时候。更高的阶数意味着更慢，因为运行时间的增长速度远大于其输入数据的大小。

　　需要注意，尽管大O已经是一个分析利器了，但它不能代替分析器，因为分析器可以运行代码以找出瓶颈所在，它仍是不可或缺的。但是，了解大O分析以及代码如何随着数据增长而变慢，可以让你避免编写本不该慢的代码。